Introduction
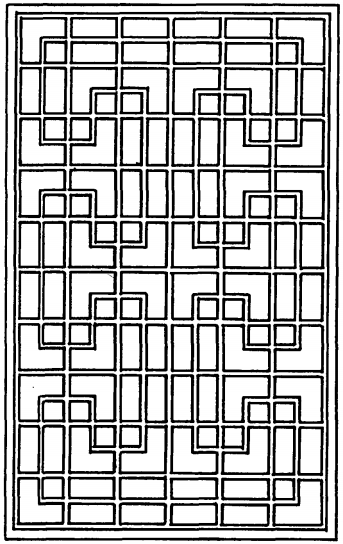Having worked on Islamic Star Patterns and Celtic Knots, I wondered where else I could find other art systems that could be procedurally generated. In 2018 (according to a screenshot I have), I came across George Stiny's paper on a different kind of lattice window,
which he called ice-ray. Although I wasn't too keen on this kind of pattern or the
shape-grammar method, his introduction contained the figure to the right. He writes nothing
about it in the article, but it immediately struck me as some kind of Hilbert-curve. I didn't do anything with it, but I'll come back to it later.
He did also reference an old book by a guy named Daniel Sheets Dye, which is fortunately available on Open-Library! I finally decided to work on this idea in December 2019, first reading through the book and seeing if the space-filling curve had any merit or whether a different system would come to mind. I did come up with two systems I was happy with and here is the result.
Important to note is that these two systems (and the third addition) aren't intended to be historically accurate nor to produce every kind of pattern. The design space of patterns isn't limited to these algorithmic formulations, but I think it is useful to explore the various constraints regardless - not only can we easily generate good examples that do appear in the real world, but the underlying systems can be extended or modified to create new and unexpected patterns.
System 1: Square Merging
The first system is simple, but very effective. You start with a grid of squares, and you just merge adjacent squares in each step. By itself, this isn't enough, but you can add a few different constraints and the patterns soon look pretty cool.
One constraint is to limit the number of merged squares to, say, 4. This is the Tetris number! For some reason, there are too many different shapes with 5 squares, too few with 3 squares, and the result is not as aesthetically pleasing. 4 is just right! You can make this a hard constraint and try to make every single group contain exactly 4 squares, but this is probably an NP-Complete problem, so a soft constraint of merging with at most 4 squares will do.
Another constraint is to merge squares only in the same ring around the center, say (although the book also has a couple of examples with only vertical merges). This is enough to generate pleasing and "real" examples as well.
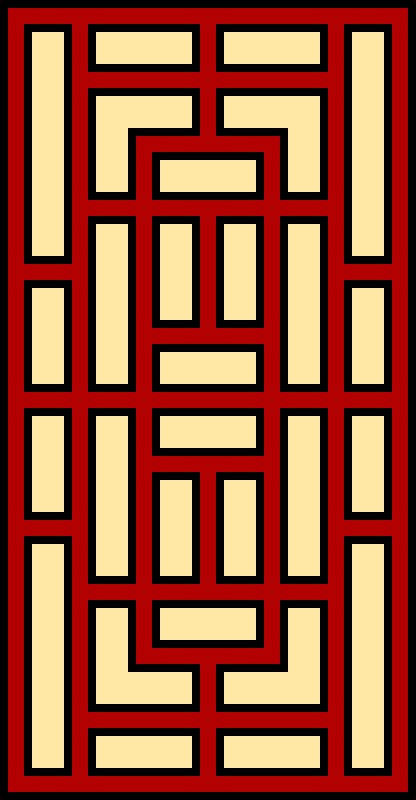
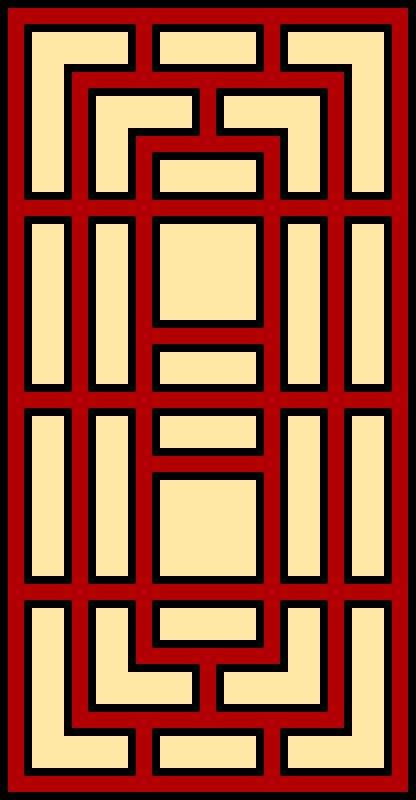
Given the last constraint, an idea is simply to flip it on its head - merge only squares that are not in the same ring.
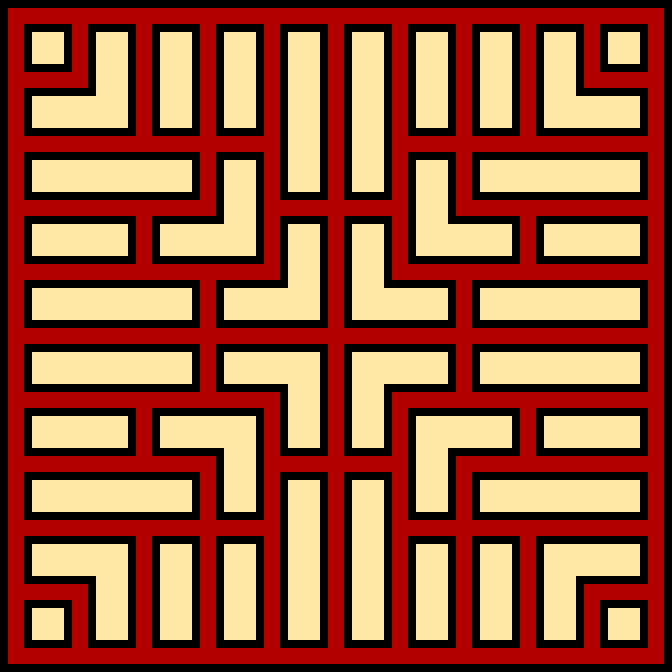
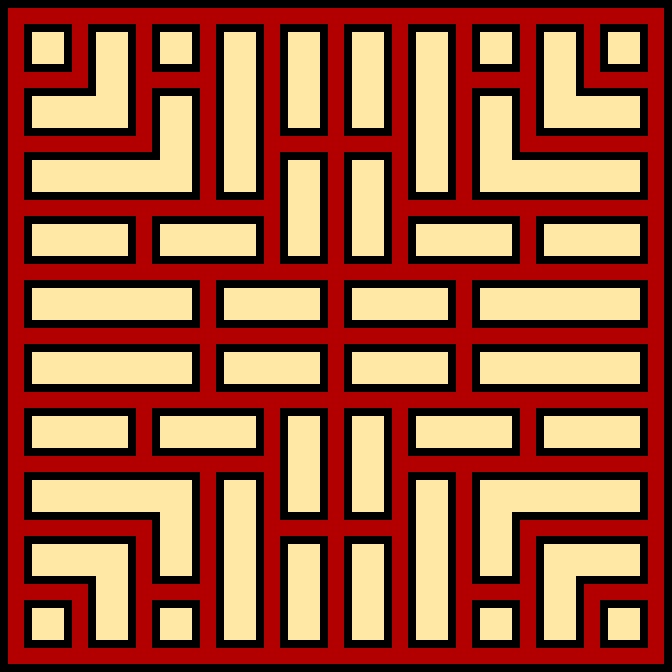
Finally, and this should go without saying, every pattern will have some kind of symmetry applied (mirror or rotational). And you can always combine the above constraints.
System 2: Overlapping Tilings
The second system is also pretty simple, but it requires more interaction to work and is also a bit more limited in the patterns it produces. Basically, you just generate a simple tiling of squares, octagons, and squares, and then you either make each polygon larger so that they overlap. You can also overlap the dual tilings (which are the same, in the case of squares and octagons), where each vertex becomes a polygon. Again, not as versatile, but it does manage to reproduce a different kind of "real" patterns - all four of patterns below appear in the book (and there are other examples that start from such patterns but then change them in a less systematic way).
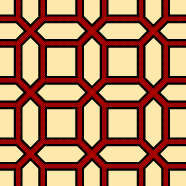
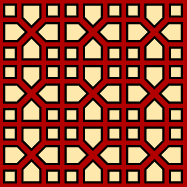
It can also be extended to produce very different patterns if you allow different edge widths, rotations, and so on. It's a bit messier to work with and easy to create overcrowded patterns, but some of the examples are pretty cool.
System 3: Space-filling Curves, Hamiltonian Cycles, MSTs
When I first worked on this problem, I didn't end up doing anything with the space-filling idea - I didn't find any other curve that would work other than Hilbert's - and the Hamiltonian Cycles seemed too messy to code, even in the specific case of grids (especially if I wanted to add other constraints). And, given that the above two systems worked pretty well, I wrapped things up and moved on.
Interestingly, as I prepared write this (in February 2021), it occurred to me that I didn't need to find Hamiltonian Cycles on grids; I could just find a Minimal Spanning Tree (MST) and then transform it into a Hamiltonian Cycle by expanding the edges and vertices into squares! I am not currently planning to implement this, but I like the idea anyway. Even though the example by Stiny above isn't doesn't exactly cover every (implied) vertex, it seems a promising path to explore.
Update: after a bit of thinking, the example is not quite a Hamiltonian Cycle, but it suggests a more complex constraint of the Square Merge system. For example, merge cells into a two groups and forbid any 4-square (a square made of 4 cells) to belong to the same group. Perhaps a SAT-enconding would be ideal to test different kinds of subconstraints. Well, maybe one day! Another update: the encoding is actually extremely simple! Since there are only two groups, we can let "true" be group 0 and "false" be group 1. Then, all we need is two constraints for each cell in the grid, stating that at least one must be true and at least one must be false of the cells: itself, to the right, below, below and to the right. Since it is this simple, I may encode it for a few grid sizes. Also, this kind of method seems related to pixel-based texture synthesis methods as well as the popular wavefunction collapse algorithm.