Introduction

This was one of my favourite projects to work on. As usual, it had a long incubation time with me discovering various facets of these ideas (including Edwin Abbott's Flatland, Rudy Rucker, Shape of Space, Miegakure, and so on), but I finally decided to implement it in August 2017 while reading Max Tegmark's Out Mathematical Universe.

This project was about answering the question "How to visualize 4 dimensional space?". First, I wrote a quick python script to project (a projection is what happens with a cube's shadow on a 2D wall, or 3D graphics on your 2D monitor) a tesseract, recreating the very famous animation - but this didn't work at all for the more complex polytopes. Where an icosahedron (3D) has 20 faces and a tesseract (simple 4D) has 24, a 600-cell (complex 4D) has 1200. You can see the messy result below! So I switched to a cross-section approach, basically an intersection of a 4 dimensional object with 3D space. Up to this point, I had only used Game Maker: Studio, which is mainly a 2D tool, so I learned Unity in the process.

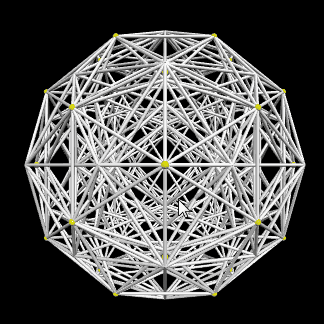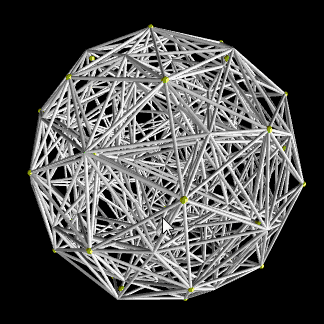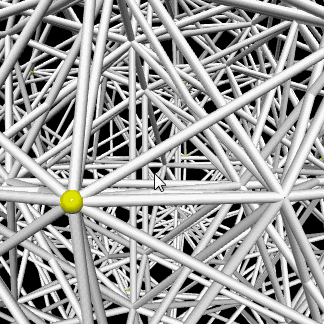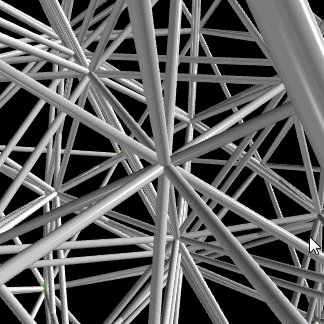
Note: the tesseract animation on the left comes from wikipedia, since I've lost the python files. The other two are files I still had.

How does it work?

The idea of a cross-section is extremely simple: you simply render the part of the objects that "lives" in our 3rd dimension. What does that mean? Well, it means whichever part of it has the z-coordinate equal to 0. One way to think about it is to use a 3D-to-2D analogy. Imagine a cube with a sheet of paper crossing through it - but you only see the piece of paper. By moving the cube around, what you see you change. The examples below are from CuriosaMathematica.

One extremely useful resource to me, at the time, was Eusebeia. I used only regular polychora, and I got the vertices from there. The algorithm goes as follows:

• (Preprocessing) Reconstruct edges and faces from the vertice data;
• Compute every edge intersection with the volume z=0;
• Apply a convex-hull algorithm;
• Color the resulting polyhedron.

My contribution has definitely been the use of the convex-hull. Computing the cross-section "by hand" seemed rather messy (and difficult to think about in 4 dimensions!), but a convex-hull is a conceptually very simple solution. Plus, it actually ran smoothly in real-time, so I was able to play around even with the most complex objects!

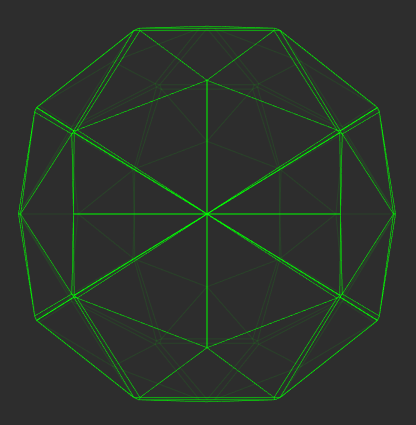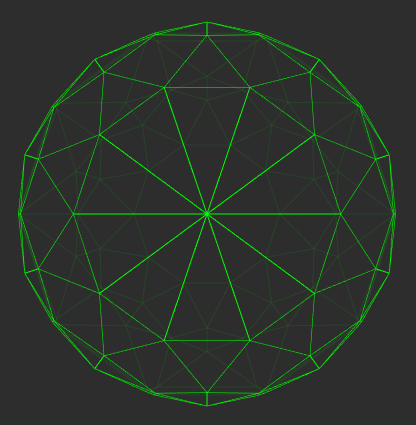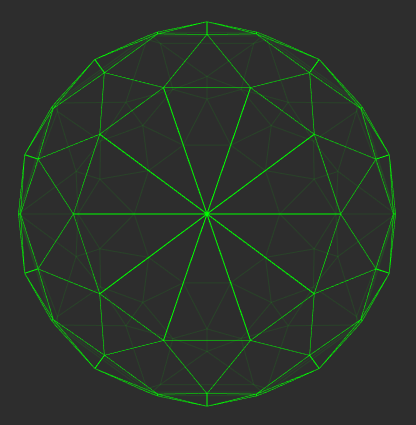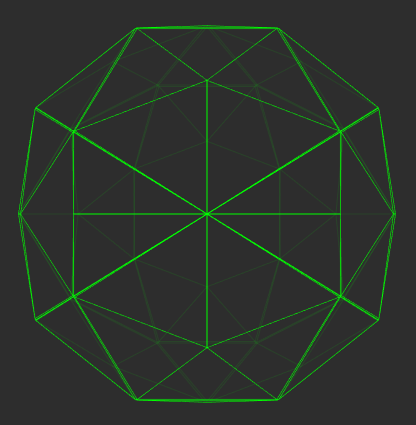
The first figure, of the left, shows a 600-cell centered at (x,y,z,w)=(0,0,0,0) but rotating in the z coordinate. Going back to the cube, imagine it rotating "forward" - it would never disappear, but its shape on the sheet of paper would change. The second and third figures show a a 600-cell and a 120-cell, respectively, crossing the volume z=0 from the outside.

Coloring

The purpose of color, beyond looking prettier, is to convey some information about the underlying symmetry of the objects. I used two different coloring systems:

• Color by face-size;
• Color by cell of origin.

Coloring by face-size is easiest - where face is the 3D face of the convex-hull, not the original object. It requires less information and still preserves the symmetries, but it definitely loses some information about the original object. A hue is simply assign from 0 to whatever maximum area seems approptiate.

Coloring by cell of origin is harder, since the convex-hull only has information about edges and vertices, not faces or cells. Fortunately, by storing additional information (like which faces and cells are incident to an edge and vertice), I was able to recover the information I needed about the color of the original cells and faces! I assigned, if I recall correctly, a hue depending on the origin cell's centroid.

The first two figures on the left are of a 600-cell rotating and crossing into the third dimension, respectively, while the last, on the right, is a 120-cell crossing into the third dimension.

Beyond

There's a lot more you can do this with idea. If you're feeling trippy, you can always place yourself inside the object!

The method can obviously be generalized to either dimensions, different geometries (hyperbolic or spherical) and also tilings. One of the most mind-blowing things I found out was de Bruijn's construction showing that you can get a by a kind of projection from a 5-dimensional tiling.